|
| | Matematičke više dimenzije |  |
| | | Autor/ica | Poruka |
|---|
Procyon
Totalno relaxiran


 
Broj postova : 1261
Godine : 34
Datum registracije : 26.07.2010
 |  Naslov: Matematičke više dimenzije Naslov: Matematičke više dimenzije  15.09.10 15:38 15.09.10 15:38 | |
| O višim dimenzijama ima spomena svugdje, od viših duhovnih dimenzija, pa više dimenzije svijeti, onda višestruke dimenzije svemira i još. Otvorio bih uvodnu riječ o matematičkim višim dimenzijama, koje su temelj za pojavu višedimenzionalnosti u teoriji struna. Mislim da je dobro početi sa 4D konveksnim poliedrima. Prvo neke definicije: Dimenzija prostora ili objekta je definirana minimalnim brojem koordinata koje su potrebne da se specificira bilo koja točka unutar tog prostora. Dimenzija koordinatnog sustava kojeg smo crtali u školi je 2. Da bismo opisali bilo koju točku unutar tog koordinatnog sustava, potrebno je odrediti na kojoj x i y koordinati se nalazi. Koordinatni sustav u prostoru je 3D sustav, potrebne su 3 koordinate da opišemo položaj neke točke unutar tog sustava. Koordinate točaka zapravo opisujemo skalarima, točnije vektorima nekog sustava. Takav sustav naziva se vektorskim prostorom. Vektor je veličina koja ima pravac, smjer i duljinu. Skalar je samo duljina tog vektora, broj. U vektorskom prostoru postoje vektori koji tvore bazu tog prostora, jedinični vektori. To su vektori čija je skalarna duljina jednaka jedan, osnovni vektori. Da bismo odredili dimenziju vektorskog prostora, trebamo odrediti koliko se linearno nezavisnih baznih vektora može nalaziti u tom prostoru. Dakle, u koordinatnom sustavu na papiru imamo 2 linearno nezavisna vektora, x i y, te je takav vektorski prostor dvodimenzionalan. Trodimenzionalan prostor bi bio onaj u kojem imamo 3 linearno nezavisna vektora pomoću kojih bismo mogli opisati bilo koju točku unutar tog prostora. Višedimenzionalan prostor je onaj u koje imamo više od 3 linearno nezavisna vektora pomoću kojih možemo opisati bilo koju točku unutar tog prostora. A sad definicije za tijela koja se promatraju. Pravilni poligoni su 2D matematička tijela koja imaju sve vanjske rubove jednake duljine i kod svakog vrha se nalazi jednaki kut. Primjeri pravilnih poligona su jednakostranični trokut, kvadrat, pravilni peterokut, pravilni šesterokut... Ima ih beskonačno. Poliedar je 3D tijelo čije su sve stranice jednake, a njegove stranice su pravilni poligoni. Konveksno tijelo je ono tijelo unutar kojeg bismo bilo gdje mogli odabrati 2 točke, A i B, te kada bismo ih spojili, ta dužina u nijednom svom dijelu ne bi izlazila van iz tijela. Konveksnih pravilnih poliedara ima samo 5, nazivaju se još i Platonovim tijelima. Evo kako oni izgledaju:  Tetraedar je poznat kao trostrana piramida, a heksaedar kao kocka. | |
| ![[Vrh]](https://2img.net/s/t/13/07/82/i_up_arrow.gif)  | | Procyon
Totalno relaxiran


 
Broj postova : 1261
Godine : 34
Datum registracije : 26.07.2010
 |  Naslov: Re: Matematičke više dimenzije Naslov: Re: Matematičke više dimenzije  15.09.10 16:26 15.09.10 16:26 | |
| Zašto postoji samo 5 3D konveksnih poliedara? Iz jednostavnog razloga što se ostala tijela više ne mogu poklopiti i da tvore zatvoreno 3D tijelo.
Kod konveksnih poliedara vrijedi jedno pravilo, nazvano i Eulerova formula:
(Broj stranica) + (broj vrhova) - (broj rubova) = 2
Uzmimo kao primjer kocku. Kocka ima 6 stranica, 8 vrhova, te 12 rubova. 6+8-12 = 2
Tetraedar ima 4 stranica, 4 vrhova i 6 rubova. 4+4-6 = 2
Zapišimo formuli ovako:
S (strane) + V (vrhovi) - R (rubovi) = 2
Da bi se pokazalo zašto je samo 5 konveksnih pravilnih poliedara, uvode se 2 nove veličine:
n = broj rubova svake pojedine strane
Kockine strane su kvadrati, a kvadrat ima 4 ruba.
m = broj strana tijela koje se susreću kod pojedinog vrha.
Kod kocke se na vrhu susreću 3 kvadrata koji i tvore taj vrh.
Rastavimo sada kocku, oslobodimo svaku njenu stranu da stoji sama za sebe. Kocka se sastojala od 6 kvadrata koje smo sad stavili zasebno, a svaki kvadrat ima 4 ruba. Broj ruba svih tih kvadrata iznosi 6*4 = 24, dok je kocka imala 12 rubova. Recimo da tetraedar tako rastavimo. Tetraedar se sastoji od 4 jednakostranična trokuta, a svaki ima 3 stranice. 4*3=12 rubova, dok je tetraedar imao 6 rubova. Dakle, dok mi na taj način rastavimo tijelo, broj rubova se podupla. Zapišimo to ovako:
S*n = 2R
Kada smo rastavili tijelo kocke na taj način, tada smo iz jednog njenog vrha napravili 3 (kod vrha kocke se susreću 3 kvadrata koji tvore taj vrh, kada ih mi razdvojimo, tada imamo 3 razdvojena vrha svakoh od kvadrata koji su bili spojeni i tvorili taj vrh. Kocka ima 8 vrhova, a svi kvadrati imaju 6*4=24. Tetraedar ima 4 vrha, kod svakog nastanu 3 nova kada se razdvoji, te razdvojeni tetraedar ima 3*4=12 vrha. Primjećujemo da je broj vrhova i rubova rastavljenih tijela isti, logično. Zapišimo to ovako:
V*m = S*n = 2R
Ovo bi trebalo vrijediti za svaki konveksni poliedar bez obzira na broj stranica.
Sada formulacija i izlučivanje:
S*n = 2R
S = 2R / n
V*m = 2R
V = 2R / m
To se uvrsti u početnu formulu:
S + V - R = 2
2R/n + 2R/m - R = 2 ; Pokrata sa 2R
1/n + 1/m - 1/2 = 1/R
Broj rubova nikad ne može biti negativan, tako da je na desnoj strani uvijek pozitivan broj, uzimajući to u obzir jednadžba se nadalje zapiše ovako:
1/n + 1/m - 1/2 > 0
1/n + 1/m > 1/2
Ovo je formula koja treba biti zadovoljena kod svih pravilnih konveksnih poliedara.
Ni n niti m ne mogu biti manji od 3, jer se inače ne bi radilo o poliedru. Sada se može napraviti provjera počevši od n=m=3.
n=3, m=3
1/3 + 1/3 = 2/3 > 1/2 Vrijedi
Tijelo koje se sastoji od poligona koji imaju 3 ruba i kod svakog vrha se susreću 3 stranice je tetraedar ili trostrana piramida.
n=4, m=3
1/4 + 1/3 = 7/12 > 1/2 Vrijedi
Tijelo koje se sastoji od poligona koji imaju 4 ruba, a kod svakog vrha se susreću 3 stranice je heksaedar ili kocka.
n=3, m=4
Provjereno iznad da vrijedi.
Tijelo koje se sastoji od poligona sa 3 ruba i kod svakog vrha se susreću 4 stranice je oktaedar.
n=4, m=4
1/4 + 1/4 = 1/2 > 1/2 Ne vrijedi
n=3, m=5
1/3 + 1/5 = 8/15 > 1/2 Vrijedi
To tijelo je ikozaedar.
n=5, m=3
Provjereno iznad.
To je dodekaedar.
Ako se ide provjeravati za druge slučajeve, dobi se da jednakost više ne vrijedi, brojevi m i n se povećavaju, a broj s lijeve strane jednadžbe je sve manji.
Dakle, postoji samo 5 pravilnih konveksnih poliedara. | |
| ![[Vrh]](https://2img.net/s/t/13/07/82/i_up_arrow.gif)  | | Procyon
Totalno relaxiran


 
Broj postova : 1261
Godine : 34
Datum registracije : 26.07.2010
 |  Naslov: Re: Matematičke više dimenzije Naslov: Re: Matematičke više dimenzije  16.09.10 12:18 16.09.10 12:18 | |
| Sljedeće o čemu bih nešto rekao je percepcija. Mi svijet gledamo svojim očima, ali što mi zapravo vidimo? Okrenemo se, gledamo po sobi, jasno nam je da soba ima dubinu, tj. mi vidimo tu dubinu, svjesni smo je, vrata su udaljena toliko i toliko metara i mi možemo doći do njih. Jasno nam je da je svijet oko nas trodimenzionalan, visina, širina i dubina su njene dimenzije. Unatoč tome što smo mi dubine prostora svjesni, mi zapravo ne vidimo 3D, dojam dubine smo naučili iz iskustva i zato jer imamo 2 razmaknuta oka koji nam jasno daju takav dojam prostora, međutim mi gledamo 2D slike u mozgu. Nije to klasična slika iz fotića, slika koju gledamo je neke fraktalne dimenzije izmeu 2 i 3 jer imamo 2 oka, ali je u principu to slika. Kada gledamo slike na kompu, tada gledamo čisti 2D, ali nam je opet sasvim jasno što je na toj slici bilo bliže fotiću, a što dalje i teško se oteti dojmu da je to tako. To je to, naše iskustvo iz svakodnevne percepcije 3D što se na gledanju slike može i vidjeti. Tako i mi dok gledamo očima, već smo toliko naviknuli na dubinu prostora da nam se ona sasvim normalno urezala u slike stvarnosti koje gledamo. A koji je dojam dubine prostora? Ono što je dalje, to je manje, a ono što je bliže, to je veće, događa se prividna deformacija objekata iz 2D. Primjer, nalazimo se u 2D i promatramo kvadrat. Mi vidimo kvadrat, tijelo čije su sve 4 stranice jednake i sva 4 kuta su prava. Međutim, što se dogodi kada se mi prebacimo u 3D i malo zarotiramo kvadrat? Odjednom više ne vidimo kvadrat, mi vidimo... neko izobličeno tijelo, sliči na trapez. Jasno, bliža stranica kvadrata nam je veća, dalja je manja, pa kako da onda i vidimo kvadrat kada je to tako? Mi ćemo opet znati da se radi o kvadratu zbog dojma dubine iz iskustva i znat ćemo da je okrenut u prostoru pa više ne izgleda kao kvadrat, već više kao trapez. Evo, ovako nešto:  Kada bismo mi ono što vidimo pretvorili u običnu sliku, jasno bismo vidjeli kako se 2D objekti deformiraju kako se rotiraju u dubinu prostora. Sad, kako iz 2D tijela nastaje 3D? Ona se jednostavno ekspandiraju u prostor po pravilu matematike. Tako imamo kocku, tijelo obloženo sa 6 kvadrata. Svi znaju da su na kocki svi kutevi pravi, pod 90°. Dobro, štima, ali što se desi kada mi tu kocku gledamo, vidimo li da su svi kutevi 90°? Štoviše vidimo li da su joj sve stranice jednake? Bacite oko na ovu sliku:  Na lijevom donjem vrhu kocke sam označio 2 kuta. Kod kocke su svi kutevi 90°, jel da? A što su ova 2, to je 90°? Nije, niti jedan kut nije pravi, a oba bi trebala biti. Rubovi s lijeve i desne strane kocke bi trebali biti paralelni. Jesu li? Nisu, ni to nije istinuto. Pa dobro, jesu li bar sve stranice kocke jednake jer bi de facto trebale biti? Gledajte bliži kvadrat sa plavim vrhovima i dalji sa crvenim. Izgledaju li jednako? Ne, ovaj dalji kvadrat je manji. Eto primjera kako dubina prostora totalno deformira izvorni predmet, ali samo za nas, jer mi ne vidimo 3D, već gledamo 2D sliku, pa nam se kocka naizgled deformira, ali ona ionako uvijek ostaje ista, normalno. Kada bismo malo zarotirali ovu kocku, mi bismo vidli da se kvadrat sa crvenim rubovima prividno nalazi unutar kvadrata sa plavim rubovima. Za zbilja se on ne nalazi unutar plavog kvadrata, mi to samo tako vidimo zbog dubine prostora, to nam se prividno tako čini. Dakle, 2D prostor se ekspandira u dubinu, i tako imamo 3D objekte. Ista logika vrijedi i za dalje, 3D prostor se dodatno ekspandira u 4D, 4D u 5D itd, a sve u dodatnu dubinu. | |
| ![[Vrh]](https://2img.net/s/t/13/07/82/i_up_arrow.gif)  | | Procyon
Totalno relaxiran


 
Broj postova : 1261
Godine : 34
Datum registracije : 26.07.2010
 |  Naslov: Re: Matematičke više dimenzije Naslov: Re: Matematičke više dimenzije  16.09.10 12:54 16.09.10 12:54 | |
| U 4D imamo politope, oni su kao poliedri u dodatnoj dimenziji. Pravilni 4D konveksni politopi nastaju iz Platonovih tijela, pravilnih 3D konveksnih poliedara. Tih 4D politopa isto tako ima 6, a dobivaju se istim matematičkim principom kao i pravilni poliedri iz pravilnih poligona. Kako je u postu iznad spomenuto, dubina prostora naizgled deformira izvorni predmet, a u 4D imamo još jednu dubinsku dimenziju koja još dodatno naizgled deformira predmet. Štoviše imamo i više točaka nekog objekta, kao što iz kvadrata koji ima 4 točke dobimo kocku koja ima 8 točaka, u 4D se broj točaka dodatno poveća. Ne znam postoji li program koji direktno barata 4D prostorom, ali imamo 3D programe kod kojih je moguća matematička manipulacija s višedimenzionalnim prostorima (ipak je to na principu matematike). U takvom programu se izračunaju koordinate 4D tijela u 4D prostoru, a zatim se to tijelo projicira u 3D prostor da bi ga program nacrtao. To je potpuno isto kao dok mi držimo kocku iznad papira i želimo točke kocke projicirati na ravninu papira tako da na papiru imamo nacrtanu tu 'kocku'. Jednostavno se sve točke okomito projiciraju na ravninu (nižedimenzionalnu plohu od 3D), i tada imamo nacrtanu kocku na papiru, kako ju svi crtamo. Isti princip je ovdje, samo se iz 4D ide u 3D. Na taj način mi možemo prikazati 4D predmete, ali to naravno nije realan prikaz kao što kocka nije realno prikazana na papiru, to je samo projekcija tog objekta. I naravno uzmimo u obzir da mi tada taj 3D objekt dodatno projiciramo u 2D jer tako gledamo svijet našim očima. I onda na kraju mi gledamo 2D projekciju 4D predmeta. Već sam iznad prikazao kako se 3D objekt deformira kada se promatra u 2D, zamislite sad kako se deformira 4D objekt promatran na isti način! Okolnosti su lakše budući da mi iz iskustva možemo lako prepoznati dubinu prostora, tj. 3D. I onda kada mi gledamo taj 4D predmet, mi ne gledamo njega kako stvarno izgleda, već njegovu projekciju. Ono što još ovisi o izgledu bilo kojeg višedimenzionalnog tijela jest stadij rotacije tog tijela. Evo opet primjer kocke iznad. Da je ta kocka malo zarotirana ulijevo, ona nam više ne bi tako izgledala, već bi nam možda ovaj dalji kvadrat bio prividno unutar bližeg kvadrata. Izgled jako ovisi o stadiju rotacije, isto tako je i sa 4D predmetom. U jednom trenu nam izgleda lijepo, a u drugom trenu kao da gledamo totalno neki drugi predmet, a u biti gledamo isti, samo mu se rotacija malo zaokrenula kao što bi se i ovoj žutoj kocki iz posta iznad, ista stvar. Najjednostavniji 4D pravilni konveksni politop je Pentachoron, nazvan još i 5-cell, hiperpiramida ili 4-simplex. Evo kako bi taj objekt izgledao u jednom stadiju rotacije.  Pentachoron nastaje iz pravilne trostrane piramide, a u 4D prostoru ima tu dodatnu točku koja je na slici prividno prikazana unutar samog tijela. Napominjem to je PRIVIDNO tako, ta točka je dalje u 4D prostoru pa je manja, kao što su objekti manji što su dalji u prostoru. Evo rotacije Pentachorona. http://upload.wikimedia.org/wikipedia/commons/d/d8/5-cell.gif Izgleda lijepo, ali i kontraintuitivno. Pitamo se kako može prolaziti stranica kroz stranicu u rotaciji tog objekta, WTF?! Ovo što gledamo je projekcija iz 4D u 3D, kao što pojasnih iznad. Recimo da projiciramo kocku na papir, na 2D, ne preklapaju li se stranice te kocke? Evo: 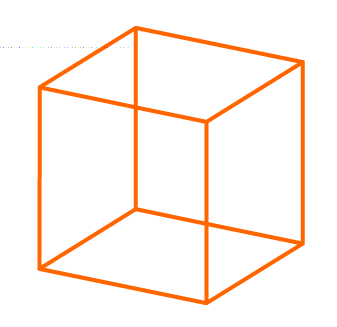 Kocka na papiru, stranica ide preko stranice, jel da? A ide li to kod stvarne kocke tako? Ne ide. I onda da gledamo rotaciju kocke na papiru, ove koju sam dao, mi bismo vidli da stranice idu jedna preko druge, a u stvarnosti uopće nije tako. Ista stvar je i sa Pentachoronom i bilo kojim 4D i višedimenzinalnim tijelom. Mi vidimo da stranica ide preko i kroz stranicu zato jer gledamo projekciju, kao što gledamo rotaciju projekcije kocke na papiru. U stvarnosti se te stranice uopće ne preklapaju, samo se nama tako čini. Još jedna zbunjujuća informacija. Objekt iznad, pentachoron, on je obložen sa tetraedrima, tj. pravilnim trostranim piramidama, to su njegove stranice kao što su stranice piramide trokuti. Mi smo intuitivno naučili da su stranice objekata (piramida, kocka itd) zapravo 2D objekti, u konkretnom slučaju poligoni. U 4D su stranice objekata zapravo 3D tijela. Da, nemoguće je to zamisliti, ali je tako. | |
| ![[Vrh]](https://2img.net/s/t/13/07/82/i_up_arrow.gif)  | | Procyon
Totalno relaxiran


 
Broj postova : 1261
Godine : 34
Datum registracije : 26.07.2010
 |  Naslov: Re: Matematičke više dimenzije Naslov: Re: Matematičke više dimenzije  18.09.10 10:22 18.09.10 10:22 | |
| Sljedeći 4D konveksni politop je Tesseract, nazvan još 8 cell, octachoron, hiperkocka ili 4D kocka. To tijelo se sastoji od 8 ćelija, i sve su kocke.  Čini se kao da se radi o "kocki u kocki", međutim to nije tako, to se nama samo tako čini gledano iz naše perspektive. Sjetimo se, gledamo 4D tijelo koje se projiciralo u 3D, i zatim se još u našem oku 3D projicirao u 2D. Na gornjoj slici sam označio jednu od kocaka, a sve ostale se mogu naći na isti princip. Kocke su jako izobličene, istina, ali to je zato jer se, za razliku od žute kocke iz 2 posta iznad, ove kocke deformiraju u još jednu dodatnu dimenziju, 4D. Kada se tijelo deformira u 2 dodatne dimenzije, ono će naravno biti deformirano, ili će barem tako izgledati, jer kocka ostaje kocka u bilo kojoj dimenziji, mi smo ti kojima se čini da se ona deformirala.  Rotacija 4D kocke može djelovati jako zbunjujuće, bez nekog smisla. Ako se pogleda malo bolje, mogu se vidjeti upravo kocke koje se međusobno rotiraju, ali su izobličene. http://upload.wikimedia.org/wikipedia/commons/5/55/Tesseract.gif https://2img.net/r/ihimizer/img135/3280/doublerotationtb6.gif https://2img.net/r/ihimizer/img138/9406/teseraktch3.gif Evo kako Tesseract izgleda gledan u nekom drugom stadiju rotacije, kada više ne izgleda kao "kocka u kocki".  Izgled ovisi o rotaciji, kao što je to slučaj kod 3D tijela, tako je i kod 4D. U jedan mah izgledaju lijepo i simetrično, u drugi zmotano i neprepoznatljivo. Kao što se kocka rastvara u latinski križ, tako se Tesseract rastvara u 3D latinski križ, ili kako god da se zove. Na slici je označeno koja kocka se zatvara sa kojom i na kojoj strani.  A evo i gif koji demonstrira kako se iz rastvorene 4D kocke opet dobi 4D kocka. https://2img.net/r/ihimizer/img250/2619/latinclosingxe5.gif | |
| ![[Vrh]](https://2img.net/s/t/13/07/82/i_up_arrow.gif)  | | Procyon
Totalno relaxiran


 
Broj postova : 1261
Godine : 34
Datum registracije : 26.07.2010
 |  Naslov: Re: Matematičke više dimenzije Naslov: Re: Matematičke više dimenzije  20.09.10 9:52 20.09.10 9:52 | |
| Hexadecachoron ili 16 cell ili je sljedeći politop. Sastoji se od 16 ćelija koje su tetraedri, trostrane piramide, to je dualni politop Tesseractu ili 4D kocki. Zašto dualni? Tesseract ima 16 vrhova, 32 ruba, 24 strane i 8 ćelija, a Hexadecachoron ima 8 vrhova, 24 ruba, 32 strane i 16 ćelija. Iste brojke, samo u drugačijem rasporedu. 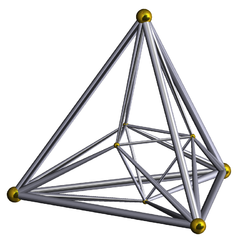 Rotacija: http://upload.wikimedia.org/wikipedia/commons/a/a0/16-cell.gif Sljedeći politop je Icositetrachoron ili 24 cell. Sastoji se od 24 ćelija koje su oktaedri, ili bipiramide. Ovo tijelo je malo kompleksnije i ima više vrhova, stranica, rubova i ćelija.  Evo i rotacija http://upload.wikimedia.org/wikipedia/commons/f/f4/24-cell.gif https://2img.net/r/ihimizer/img210/9199/24celluu7.gif E, ovdje počinju malo veći 4D politopi koji izgledaju prije svega lijepo. | |
| ![[Vrh]](https://2img.net/s/t/13/07/82/i_up_arrow.gif)  | | Procyon
Totalno relaxiran


 
Broj postova : 1261
Godine : 34
Datum registracije : 26.07.2010
 |  Naslov: Re: Matematičke više dimenzije Naslov: Re: Matematičke više dimenzije 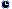 22.10.10 14:54 22.10.10 14:54 | |
| 120 cell ili Hecatonicosachoron se sastoji od 120 ćelija dodekaedra. U rotaciji izgleda jako lijepo, ali jedino imam ovo: https://www.youtube.com/watch?v=wfTsdKkrWDU Ako se pažljivije gleda, mogu se vidjeti dodekaedri u rotaciji kako se tijelo okreće.  | |
| ![[Vrh]](https://2img.net/s/t/13/07/82/i_up_arrow.gif)  | | Procyon
Totalno relaxiran


 
Broj postova : 1261
Godine : 34
Datum registracije : 26.07.2010
 |  Naslov: Re: Matematičke više dimenzije Naslov: Re: Matematičke više dimenzije 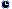 27.10.10 18:40 27.10.10 18:40 | |
| Ostao je još samo jedan, 600 cell ili Hexacosichoron. Njegovih 600 ćelija su tetraedri. Izgleda dosta komplicirano jer ima puno ćelija, rubova i vrhova.  I to su svi 4D konveksni politopi. Nakon 4D slijedi 5D na isti princip kako se iz 3D razvio 4D i tako do u n-dimenzija. U 5D nadalje ima samo po 3 i tako do n-dimenzija, bazna tijela za njih su kocka, tetraedar i križ. U 4D zapravo ima najviše pravilnih politopa (6), u 3D ih je 5, a 5D i nadalje samo po 3. | |
| ![[Vrh]](https://2img.net/s/t/13/07/82/i_up_arrow.gif)  | | mobile
VIP član


 
Broj postova : 17288
Godine : 34
Datum registracije : 23.04.2011
 |  Naslov: Re: Matematičke više dimenzije Naslov: Re: Matematičke više dimenzije  16.05.11 19:58 16.05.11 19:58 | |
| | |
| ![[Vrh]](https://2img.net/s/t/13/07/82/i_up_arrow.gif)  | | Sponsored content
 |  Naslov: Re: Matematičke više dimenzije Naslov: Re: Matematičke više dimenzije  | |
| |
| ![[Vrh]](https://2img.net/s/t/13/07/82/i_up_arrow.gif)  | | | | Matematičke više dimenzije | ![[Vrh]](https://2img.net/s/t/13/07/82/i_up_arrow.gif) |
|
Similar topics |  |
|
| | Permissions in this forum: | Ne moľeą odgovarati na postove.
| |
| |
| | Online | Ukupno je: 212 korisnika/ca online; 0 registriranih, 0 skrivenih i 212 gostiju. :: 1 Bot
/
Najviše korisnika/ca istovremeno online bilo je: 1514, dana 02.11.19 16:59.
|
| Statistics | Registriranih korisnika/ca: 6485.
Najnoviji/a registrirani/a korisnik/ca: Радослав.
Ukupno postova: 943552. in 18084 subjects
|
|



